Quad data
Simplygon supports geometry consisting partially or completely of quads, referred to as quadrilateral meshes, or quad meshes for short. Processors and tools can understand and try to preserve the additional structure present in such a geometry. This section describes data format and tools for setting up quad geometries.
The QuadFlags field
GeometryData is fundamentally a triangle-based data structure where attributes can be stored per triangle, corner or vertex. QuadFlags is a triangle field that encodes quad information onto each triangle to make it possible for Simplygon to convert to quadrilateral data internally when needed. The field is a simple char which pairs triangles forming a quad:
| QuadFlag name | value | Description |
|---|---|---|
| SG_QUADFLAG_FIRST | 0 | First triangle of quad |
| SG_QUADFLAG_SECOND | 1 | Second triangle of quad |
| SG_QUADFLAG_TRIANGLE | 2 | Regular triangle |
The QuadFlags field can only pair two consecutive triangles in the field array, so the following must be true for a quad to be valid:
- If triangle at index N is FIRST, then the triangle at index N+1 must exist and be SECOND.,
- If triangle at index N is SECOND, then the triangle at index N-1 must exist and be FIRST.
Vertex connectivity
A quad can be formed from two triangles if they share a common edge, i.e. both triangles connect at the same vertices over that shared edge. However, Simplygon is very specific in what edges from the triangles that must be shared:
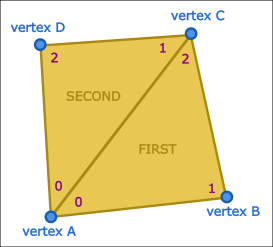
Triangles in GeometryData connect three vertices by index, so the following must be true for a quad to be valid:
- The first vertex index of the FIRST-marked triangle must equal the first vertex index of the SECOND-marked triangle.
- The third vertex index of the FIRST-marked triangle must equal the second vertex index f the SECOND-marked triangle.
- The second vertex index of the FIRST-marked triangle must NOT equal the third vertex index of the SECOND-marked triangle.
Corner connectivity
Corner fields differ slightly from vertex fields - they are unique per triangle rather than indexed. When two triangles merge to form a quad, the internal shared triangle edge will dissolve and render associated corner data redundant (Simplygon associates each triangle edge with the corner it emanates FROM).
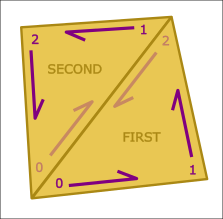
To avoid losing corner data, Simplygon takes a cautious approach when mapping corner data from triangles to quads: For a quad to be considered valid, corner data on the joining corners must match perfectly:
- All corner data on the first corner of the FIRST-marked triangle must be equal to that on the first vertex of the SECOND-marked triangle.
- All corner data on the third corner of the FIRST-marked triangle must be equal to that on the second vertex of the SECOND-marked triangle.
Validation
Simplygon provides useful tools for developers setting up QuadFlags: GeometryData::ValidateQuadFlags() checks that all constraints on quadrilateral meshes are met and logs detailed information on what is considered malformed. GeometryData::RepairQuadFlags() repairs the geometry, causing any malformed quads to revert to regular triangles.
Export
Normally, all scene exporters that support quad data will automatically export a geometry with QuadFlags to quads. This behavior can be overridden by setting the ForceTriangleExport flag on SceneExporter ( SceneExporter::SetForceTriangleExport(true) ). When set, the exporter will ignore the QuadFlags of the geometry and it will be exported as a pure triangle mesh.
Example
void AddQuadFlagsToGeometryData(spGeometryData geom)
{
// Add quad flags to the geometry data (per triangle)
geom->AddQuadFlags();
spCharArray quadFlags = geom->GetQuadFlags();
// Add quad flags to each triangle.
// In this contrieved example, every third triangle (and the next) forms a quad,
// consequently leaving one regular triangle in between each quad.
for( int t_index = 0; t_index < geom->GetTriangleCount(); t_index += 1 )
{
if( t_index % 3 == 0 && t_index < geom->GetTriangleCount() - 1 )
{
// Form a quad from two triangles
quadFlags->SetItem( t_index , SG_QUADFLAG_FIRST );
quadFlags->SetItem( t_index + 1, SG_QUADFLAG_SECOND );
t_index++;
}
else
{
// Mark as regular triangle
quadFlags->SetItem( t_index, SG_QUADFLAG_TRIANGLE );
}
}
// Validate and repair the geometry
if( !geom->ValidateQuadFlags() )
{
geom->RepairQuadFlags();
}
}void AddQuadFlagsToGeometryData(spGeometryData geom)
{
// Add quad flags to the geometry data (per triangle)
geom.AddQuadFlags();
spCharArray quadFlags = geom->GetQuadFlags();
// Add quad flags to each triangle.
// In this contrieved example, every third triangle (and the next) forms a quad,
// consequently leaving one regular triangle in between each quad.
for( int t_index = 0; t_index < geom.GetTriangleCount(); t_index += 1 )
{
if( t_index % 3 == 0 && t_index < geom.GetTriangleCount() - 1 )
{
// Form a quad from two triangles
quadFlags.SetItem( t_index , SG_QUADFLAG_FIRST );
quadFlags.SetItem( t_index + 1, SG_QUADFLAG_SECOND );
t_index++;
}
else
{
// Mark as regular triangle
quadFlags.SetItem( t_index, SG_QUADFLAG_TRIANGLE );
}
}
// Validate and repair the geometry
if( !geom.ValidateQuadFlags() )
{
geom.RepairQuadFlags();
}
}def AddQuadFlagsToGeometryData(geom):
# Add quad flags to the geometry data (per triangle)
geom.AddQuadFlags()
quadFlags = geom.GetQuadFlags()
# Add quad flags to each triangle.
# In this contrieved example, every third triangle (and the next) forms a quad,
# consequently leaving one regular triangle in between each quad.
for t_index in range( geom.GetTriangleCount() ):
if t_index % 3 == 0 and t_index < geom.GetTriangleCount() - 1:
# Form a quad from two triangles
quadFlags.SetItem( t_index , SG_QUADFLAG_FIRST )
quadFlags.SetItem( t_index + 1, SG_QUADFLAG_SECOND )
t_index += 1
else:
# Mark as regular triangle
quadFlags.SetItem( t_index, SG_QUADFLAG_TRIANGLE )
# Validate and repair the geometry
if not geom.ValidateQuadFlags():
geom.RepairQuadFlags() Simplygon 10.3.5200.0
Simplygon 10.3.5200.0